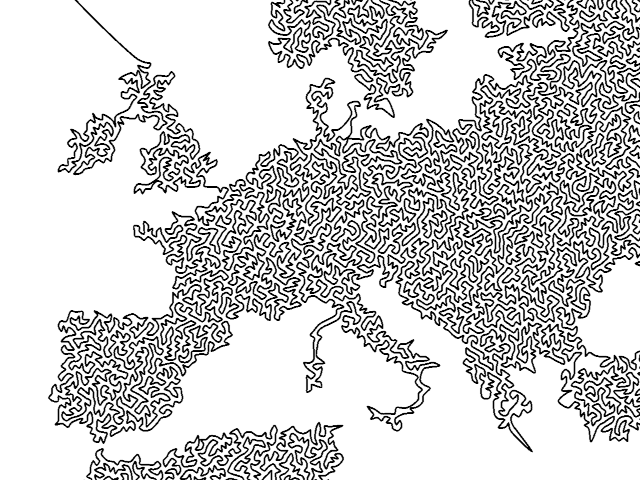
tl;dr: My hobby project FiniteCurve.com is a web app that draws an image with a single, long, non-intersecting line. This post explains the process.
Like many engineers, I’ve had a long standing fascination with mazes. One manifestation of this was elementary school drawings of ever-winding but never overlapping lines, like this:

They were fascinating to look at but tedious to draw. When I learned programming a few years later, I wrote many grid-based maze generators. However, while I’ve pondered the problem every several years since, I never ended up writing one that could replicate that organic, free-flowing, space filling style.
That is, until recently.
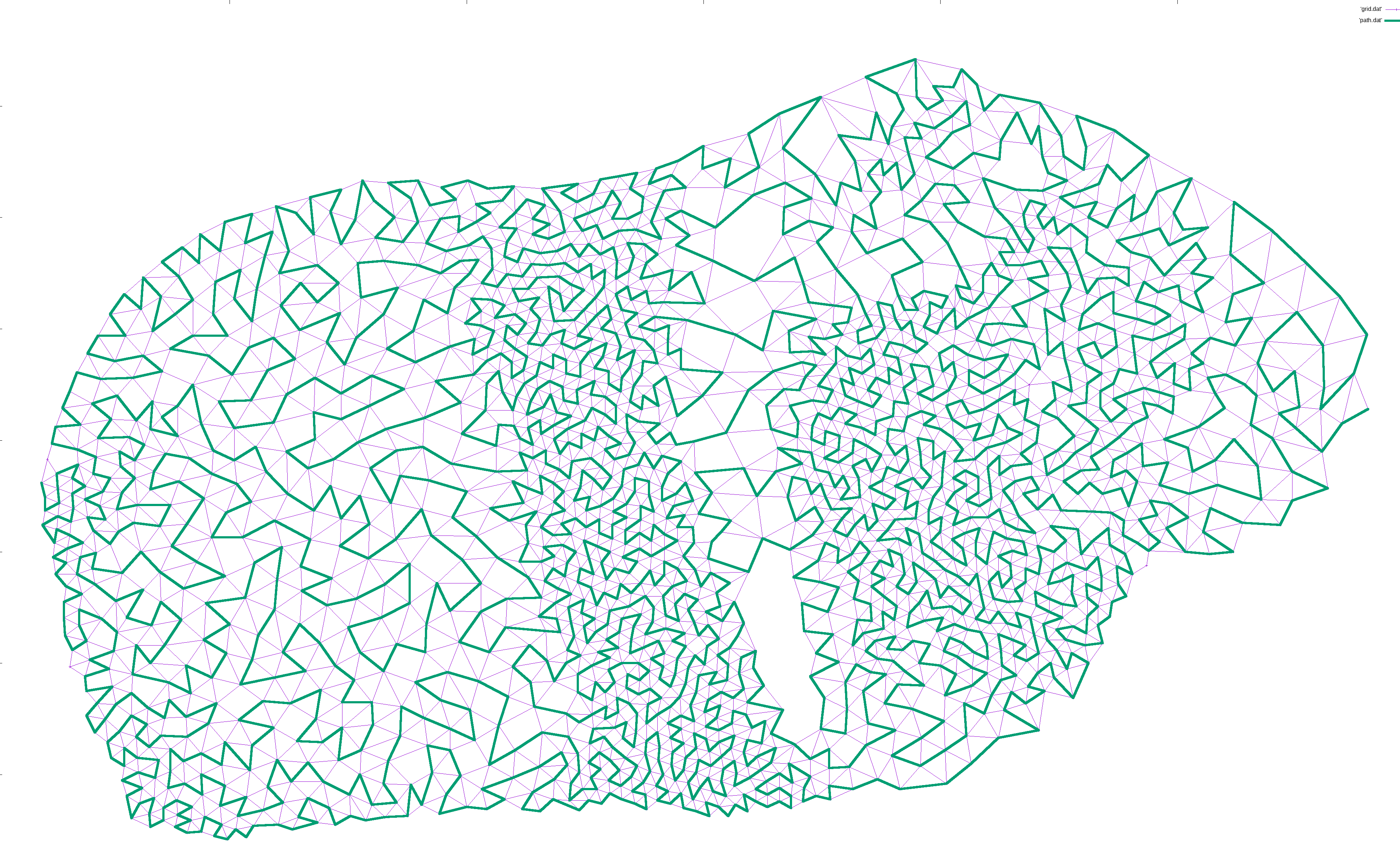
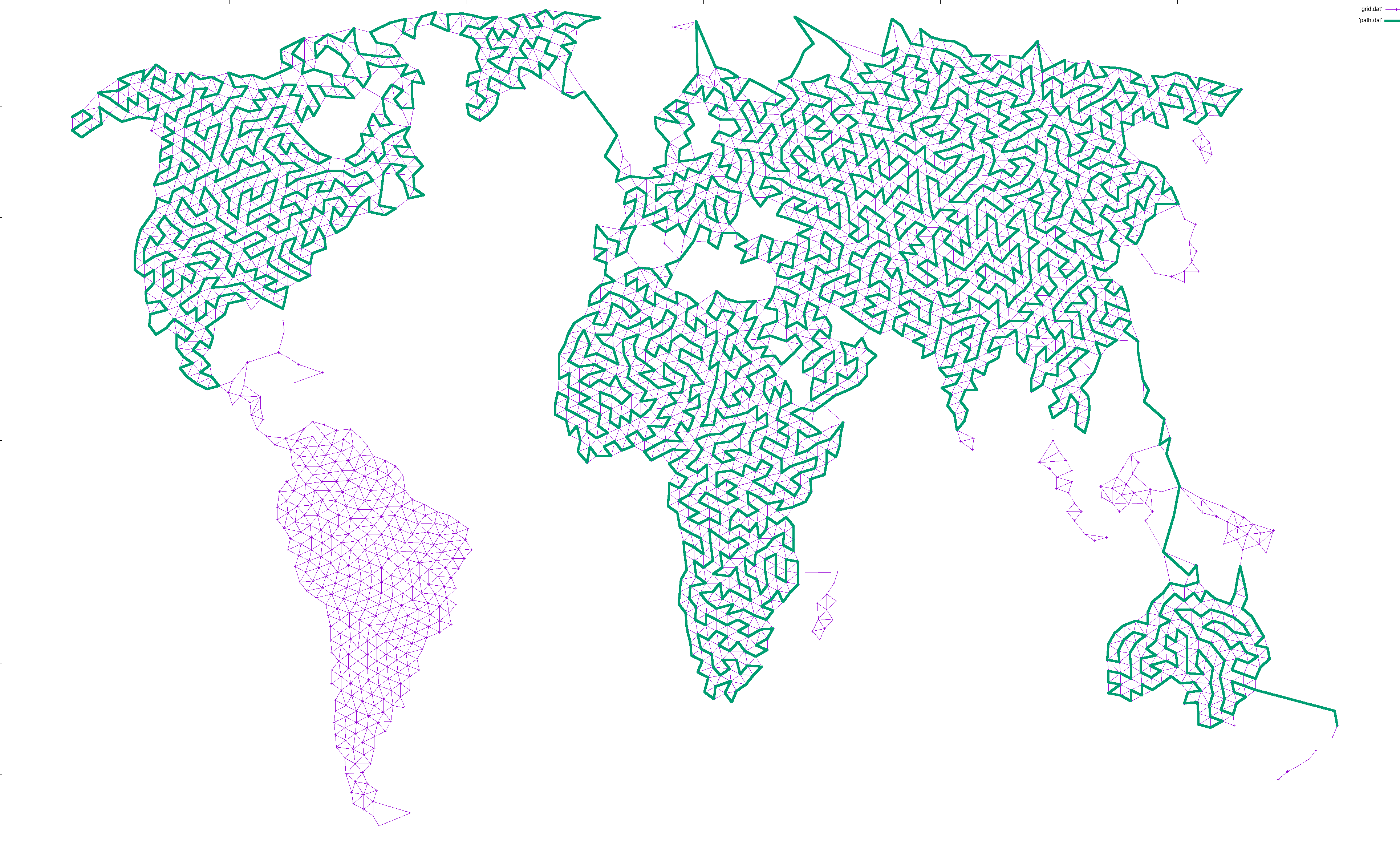
After 20 years, my pondering coincided with a blank spot on my wall, and I finally decided to implement it. Here’s Central Europe drawn with a single, ever-winding line. Click to see the entire world (10000×5000, 4MB).
The actual artwork I put on my wall — which looks better in person but doesn’t convey the concept as convincingly in a blog post — was of my guinea pig. Maze obsession aside, my favorite part is how discoverable it is:

It looks like a grayscale photo from a distance, but as you get closer you realize that it’s made up of something, thereby inviting you to get closer still until you have your nose pressed up against it, tracing the 160 meter line around.
I never intended to publish the program, but the result was striking enough that I compiled the C++ code to Wasm via emscripten, added a scrappy frontend, and put it online. You can play around with it on FiniteCurve.com. The source code is koalaman/finitecurve.com on GitHub.
I was not aware of this until I after I finished it, but this style closely resembles what’s known as "TSP art". Traditionally, it’s done by laying out points with a density according to a grayscale image, solving the Traveling Salesman Problem, and graphing the result.
Of course, even approximating TSP is hard, so generating such images takes minutes for smaller ones and days for large ones.
Since I only cared about the visual impression and not about the optimality or completeness of the resulting path, I just used some ad-hoc heuristics. The tool runs in seconds.
So how does it work?
The general approach is to generate a point cloud with a density matching a grayscale input image, and finding something close to a Hamiltonian path that doesn’t cross itself.
It’s a short description, but there are multiple noteworthy details:
- The path does not need to be short, as it would in the Travelling Salesman Problem. Arguably, the longer the better.
- The path must not cross itself. A TSP solution under triangle inequality will get this for free, but we have to work for it.
- The path does not need to be complete. In fact, it shouldn’t be. Any far-away point is better left unvisited to avoid causing unsightly artifacts. Unvisited central points will merely cause small visual glitches.
- It’s a path and not a cycle. Not because it’s easy, but because it’s hard. A visual cycle can trivially be created by tracing the circumference of a spanning tree in O(n) time, and where’s the fun in that?
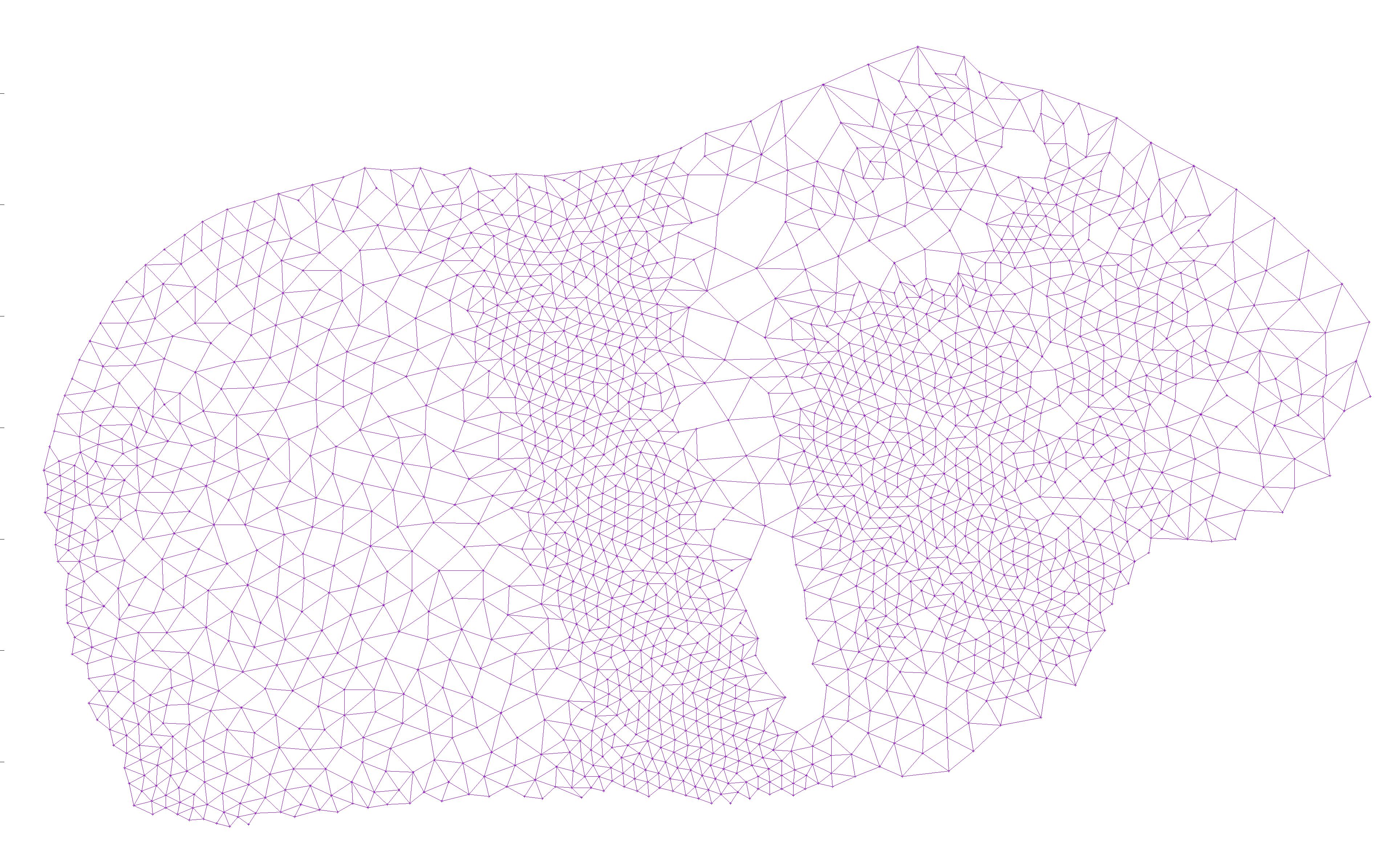
To generate a point cloud, I simply went over each pixel in a grayscale input and added a vertex there if there wasn’t already one within some distance d determined by the shade of the pixel:
I then added edges from each node to all nearby nodes, as long as the edge did not cross an existing edge. This way, there would be no crossing edges, so any Hamiltonian path would avoid crossing itself:
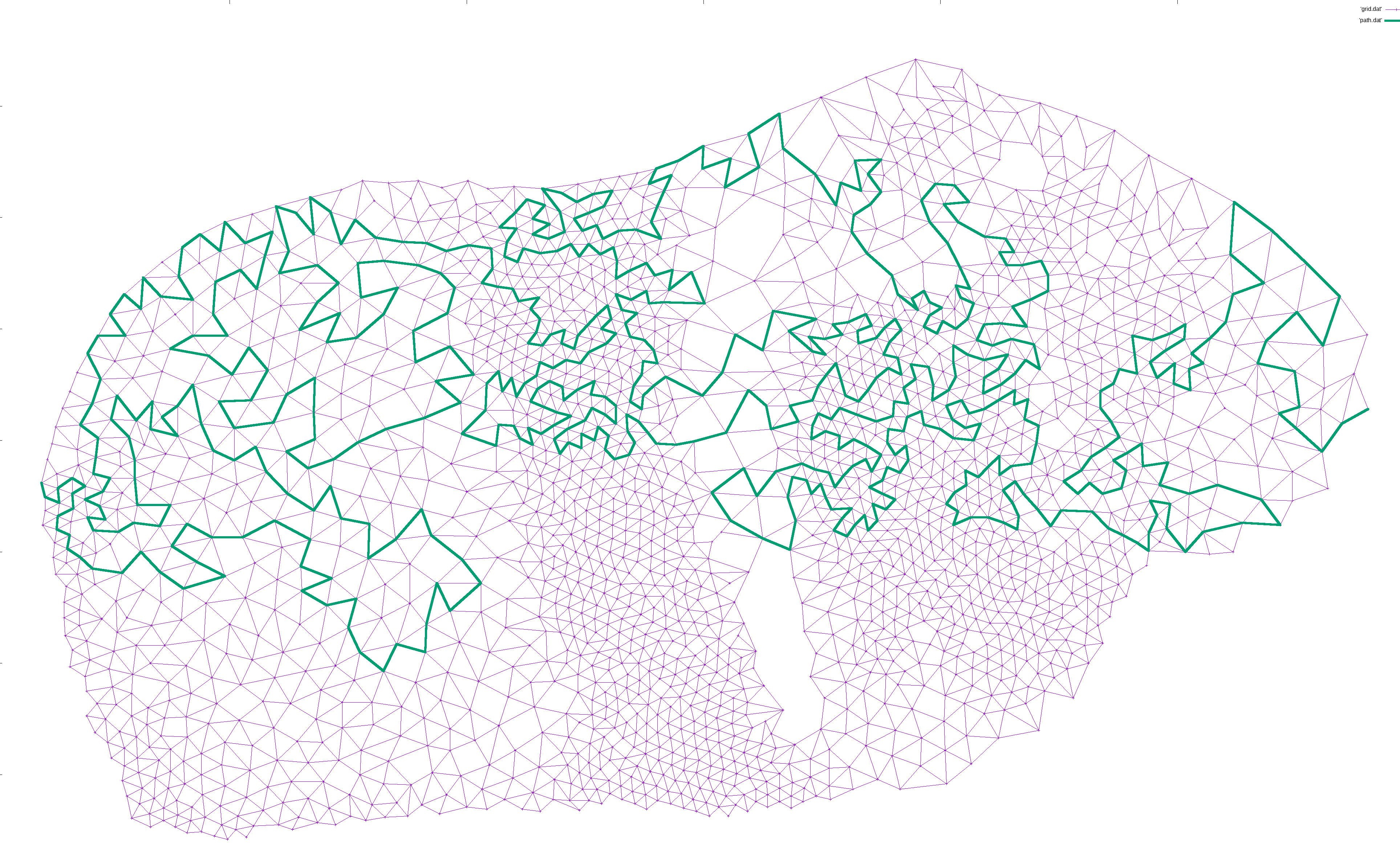
I then designated an arbitrary start point and an end point. The exact points don’t matter, but for ease of locating them, I picked the left-most and right-most points, and used plain ol’ depth first search to find a path between them:
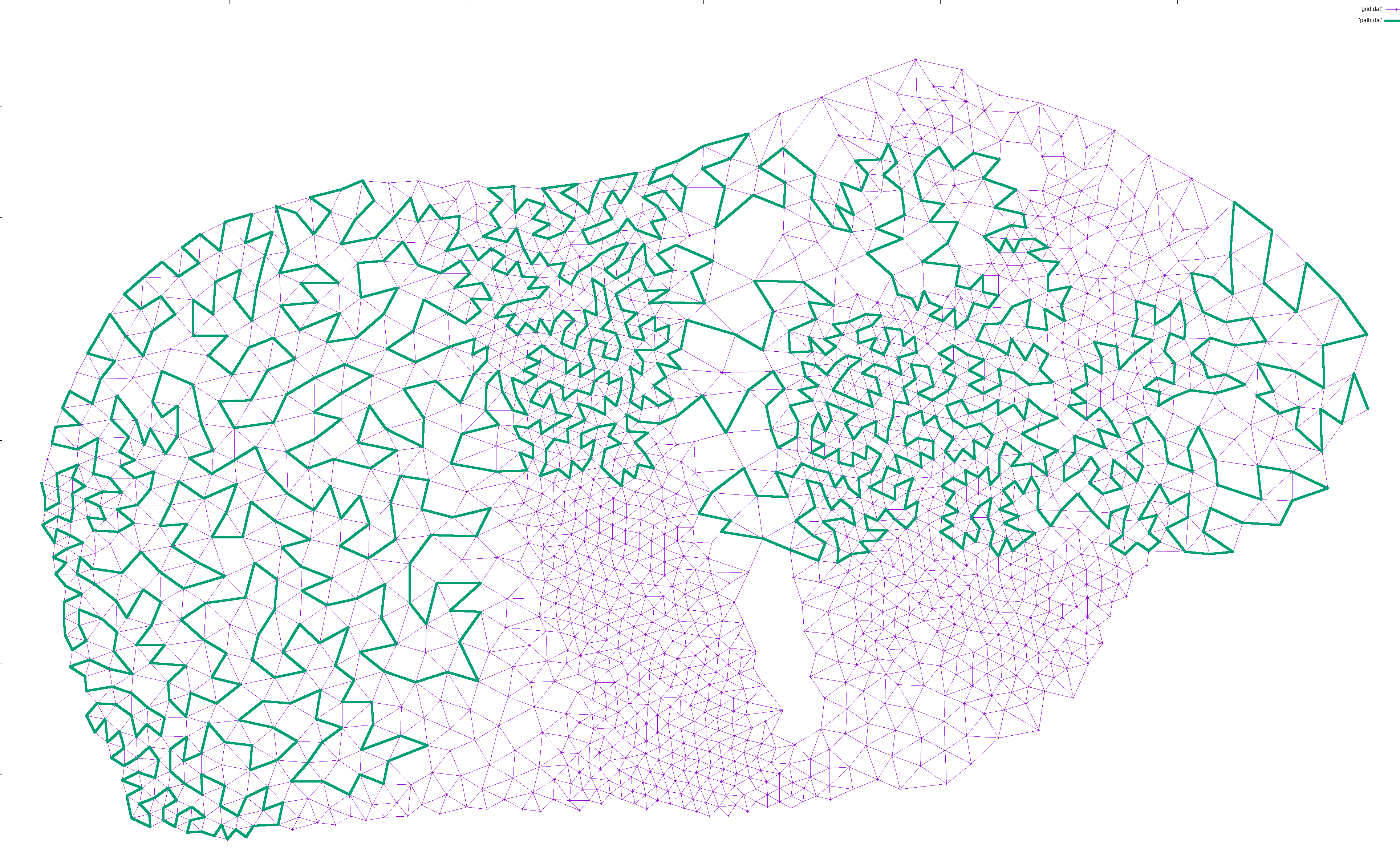
I would then iteratively expand the path. For each pair of points (p1, p2) along the path, I would find a neighbor n of p1 and try to find a path from n to p2. If found, I would expanded the path from p1->p2 to p1->n->...->p2, which is guaranteed to be longer in terms of nodes. This way, the path gradually lengthened to cover most of the nodes:
This is enough for well connected graphs.
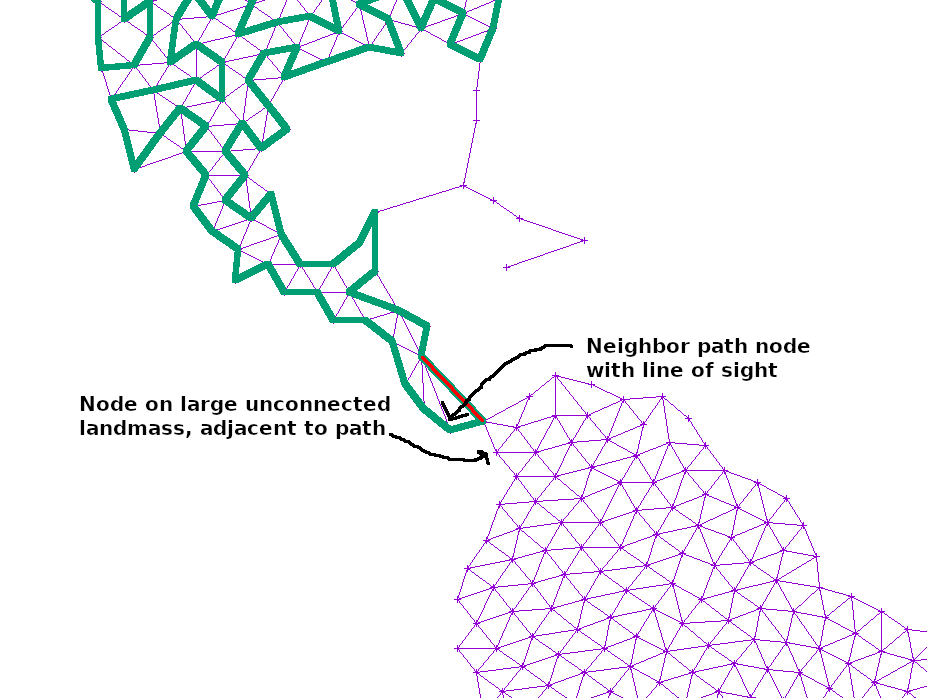
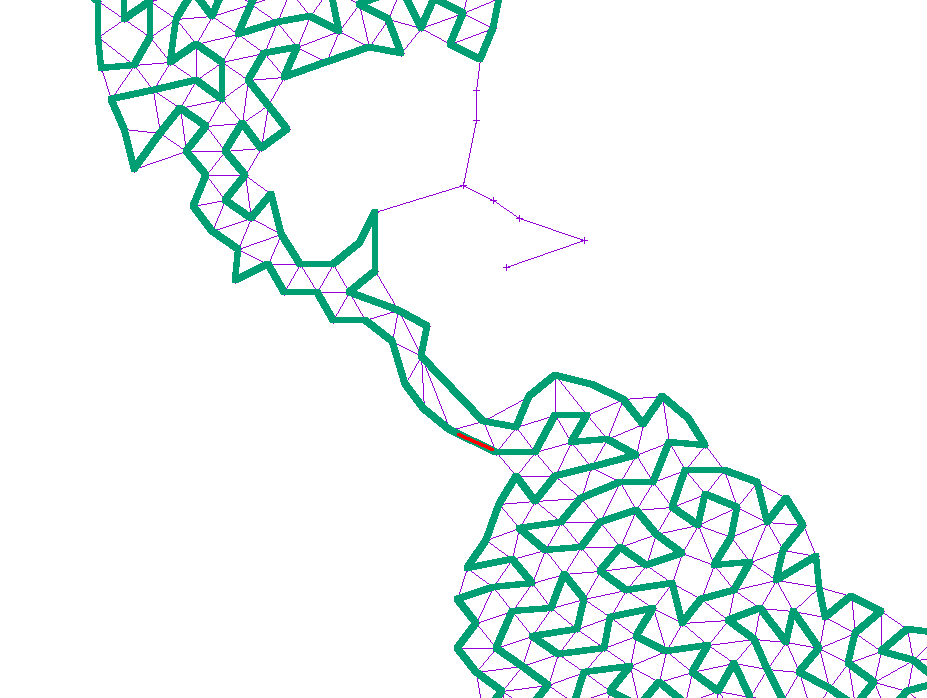
For disjoint graphs, such as a world map, I simply added the shortest edge that would connect the disjoint regions together. This ensures that a path exists between the start and end, but necessarily leaves large island unconnected since there is only a single bridge there:
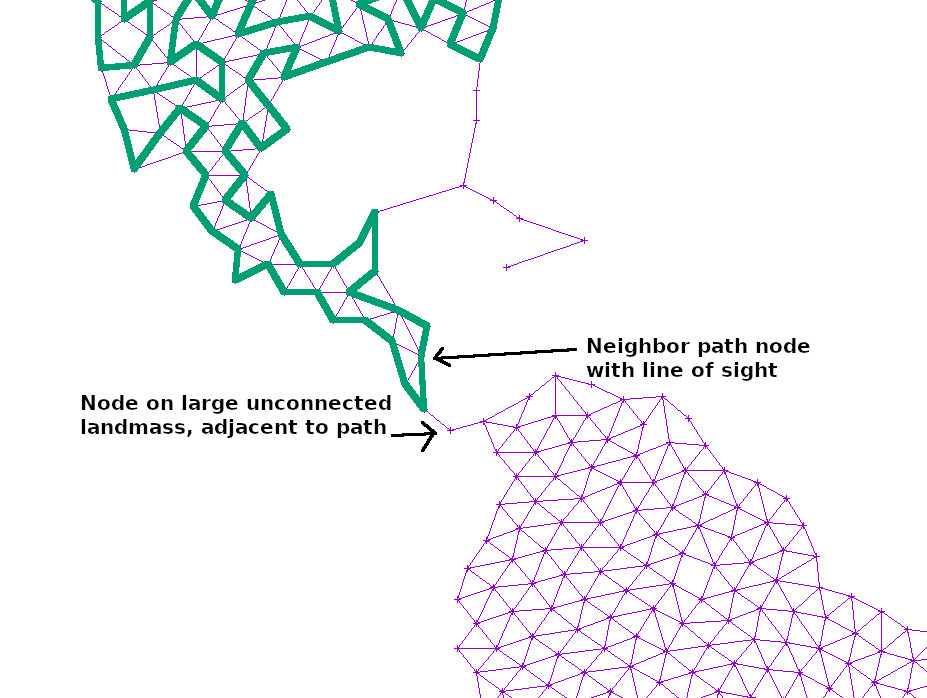
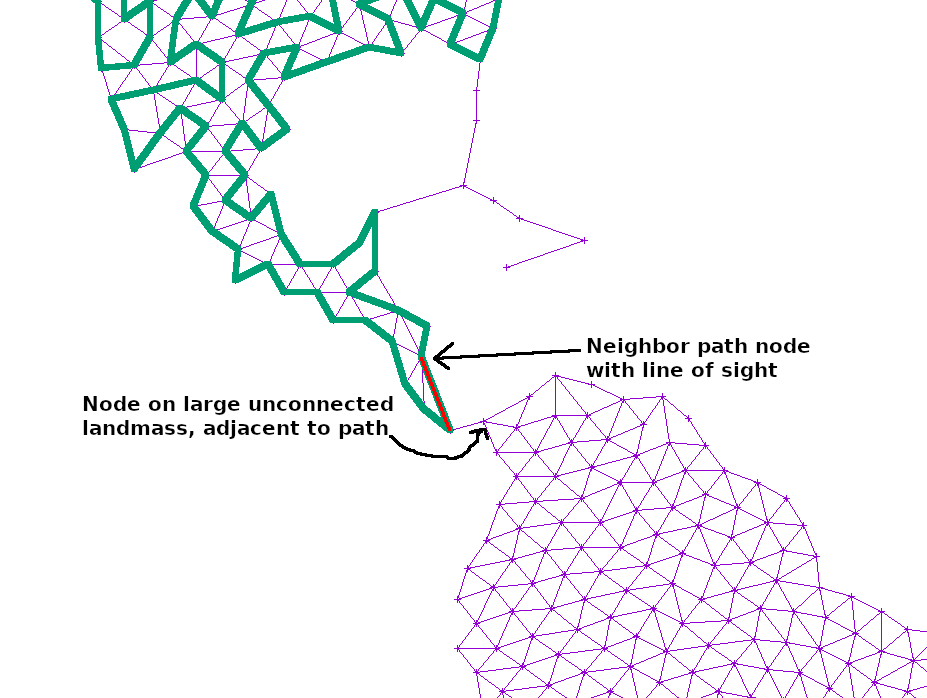
If the path at any point touched a large, unexplored section of the graph, I simply added another edge from the neighbor or neighbor’s neighor to that point. That way, any such island would slowly become reachable:
Finally, the curve is smoothed from simple, linear segments into Catmull–Rom splines, and then mapped into Cubic Bezier splines that can easily be rendered in SVG.
There is some additional polish like ignoring areas under a certain size or that are just a long, thin line of points, shuffling to try to avoid holes in the middle of a graph, and pruning edges coming out of a single vertex that are too close in angle, but really — that’s it.
I had a lot of fun hacking this project together, and I still find the result fascinating and captivating. Give it a spin on FiniteCurve.com and see what you think!
(Thanks to gnuplot for its ever invaluable plots, both for debugging, and for the illustrations in this post)